物质对β射线的吸收分析(试验论文)
来源:本站 作者:常州锐奇精密测量技术有限公司 发布时间:2020-05-15 17:42:47 浏览量:2701实验目的:
是学习和掌握与物质对射线吸收的有关知识和实验方法,测量吸收曲线并求出β射线的射程和大能量。同时进一步加深对计数管、定标器等仪器的了解。
实验仪器:
G-M计数管、放射源、薄铝箔、厚铝箔。
实验原理:
当能量的β射线(即高速电子束)通过物质时,与该物质原子或原子核相互作用,由于能量损失,强度会逐渐减弱,即在物质中被吸收。电子与物质相互作用的机制主要有三种:
一,电子与物质原子的核外电子发生非弹性碰撞,使原子激发或电离,电子以此种方式损失能量称为电离损失。电离损失的能量损失可由下式给出:
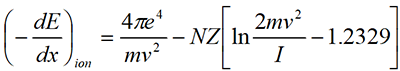
此式适用于非相对论情况,式中v为电子速度,N、Z、I分别为靶物质单位体积内的原子数、原子序数、平均激发能。由此看出,电离损失的能量与入射电子的速度、物质的原子序数、原子的平均激发能等因素有关。
二,电子受物质原子核库仑场的作用而被加速,根据电磁理论作加速运动的带电粒子会发射电磁辐射,称为轫致辐射,使电子的部分能量以X射线的形式放出,称为辐射损失。这主要在能量较高的电子与物质相互作用时发生。辐射损失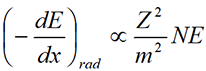 式中m、E分别为入射电子的质量、能量,Z、N分别为靶物质的原子序数和单位体积中的原子数。
式中m、E分别为入射电子的质量、能量,Z、N分别为靶物质的原子序数和单位体积中的原子数。
除以上两种能量损失外,β射线在物质中与原子核的库仑场发生弹性散射,使β粒子改变运动方向,因电子质量小,可能发生比较大角度的散射,还可能发生多次散射,因而偏离原射束方向,使入射方向上的射线强度减弱,这种机制成为多次散射。如果散射角超过90°,这种散射称为反散射。
β射线通过物质时主要以上述三种相互作用方式损失能量使强度减弱。发生三种相互作用的概率与β粒子的能量、吸收物质的原子序数等因素有关。
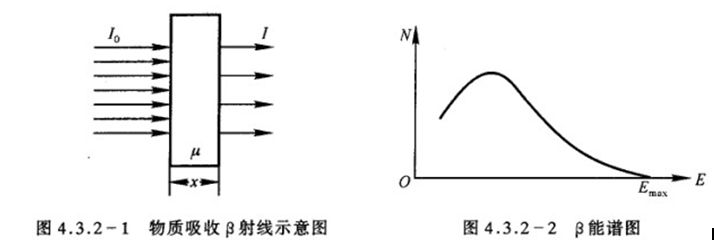
考虑一束初始强度为I0的单能电子束,当穿过厚度为x的物质时,强度减弱为I,其示意图
强度I随厚度x的增加而减小且服从指数规律,可表示为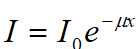 式中μ是该物质的线性吸收系数。实验指出,不同物质的线性吸收系数有很大的差别,但随原子序数Z的增加,质量吸收系数
式中μ是该物质的线性吸收系数。实验指出,不同物质的线性吸收系数有很大的差别,但随原子序数Z的增加,质量吸收系数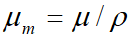 (ρ是该物质的密度)却只是缓慢地变化,因而常用质量厚度
(ρ是该物质的密度)却只是缓慢地变化,因而常用质量厚度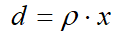 来代替线性厚度x,原子核β衰变放出高速电子的同时,还放出中微子,因此放出的电子并不是单一能量的,而是具有各种能量分布的连续能谱,因此β射线的吸收曲线并不准确地服从指数规律。
来代替线性厚度x,原子核β衰变放出高速电子的同时,还放出中微子,因此放出的电子并不是单一能量的,而是具有各种能量分布的连续能谱,因此β射线的吸收曲线并不准确地服从指数规律。
从图中可以看出,有一大能量Emax,不同的核发生β衰变时,放出的电子能谱的Emax值不同,常以Emax代表β射线的特征能量。某些放射性核素会同时发射几种大能量不同的β射线,这就会使实验得到的吸收曲线更为复杂,放射性核素β衰变还可能伴随γ射线,加之轫致辐射的影响,伴有X射线,使吸收曲线的尾部偏离指数规律,具有大能量的β射线,在具有吸收系数的物质中所能穿过的大厚度,称为该射线在该物质中的大射程。通常定义通过吸收物质后,射线强度降低到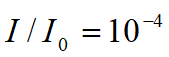 时,所对应的吸收物质厚度d即为β射线的射程R。
时,所对应的吸收物质厚度d即为β射线的射程R。
在实际测量中吸收曲线的尾部由于γ射线和轫致辐射的存在而变平,因此只能根据曲线变平之前的下降趋势按直线外推至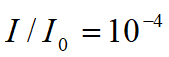 处,从而得到β射线的射程R。Β射线的射程与β射线的大能量之间,有经验公式相联系,如吸收物质是铝,则当射程
处,从而得到β射线的射程R。Β射线的射程与β射线的大能量之间,有经验公式相联系,如吸收物质是铝,则当射程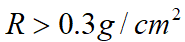 时,
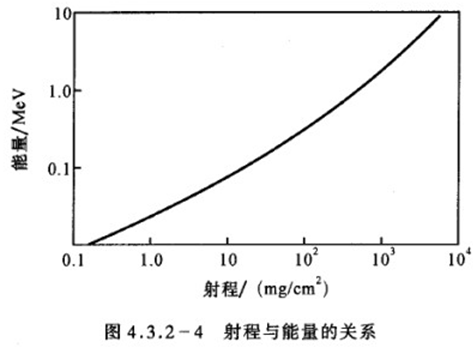
时, 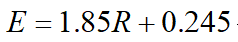 式中E为β射线的大能量,单位为MeV。当用质量厚度表示射程R时,对于原子序数相近的物质,射程也近似相同。公式(5)不仅对铝适用,对那些原子序数与铝相近的物质也是适用的。图4.3.2-4给出β射线的射程R与其能量E之间的关系曲线,通过该曲线也可由射程求出对应的能量,或由β射线的能量找出对应的射程。该图的坐标轴均取对数坐标。
式中E为β射线的大能量,单位为MeV。当用质量厚度表示射程R时,对于原子序数相近的物质,射程也近似相同。公式(5)不仅对铝适用,对那些原子序数与铝相近的物质也是适用的。图4.3.2-4给出β射线的射程R与其能量E之间的关系曲线,通过该曲线也可由射程求出对应的能量,或由β射线的能量找出对应的射程。该图的坐标轴均取对数坐标。
数据处理及结论:
1. 铝箔的测量
铝箔的测量 | |||
长/cm | 宽/cm | 质量/mg | |
薄片 | 6.3 | 4.7 | 557.78 |
厚片 | 6.2 | 5.3 | 3550 |
2. 测量β射线密度与铝箔厚度的关系
铝箔质量厚度/mgNaN-2 | 薄片 | 厚片 | 计数 | 测量时间/s |
1b+0h | 1 | 0 | 12232 | 30 |
2b+0h | 2 | 0 | 11285 | 30 |
3b+0h | 3 | 0 | 10157 | 30 |
4b+0h | 4 | 0 | 9517 | 30 |
5b+0h | 5 | 0 | 8914 | 30 |
6b+0h | 6 | 0 | 8409 | 30 |
6b+1h | 6 | 1 | 5746 | 30 |
6b+2h | 6 | 2 | 3609 | 30 |
6b+3h | 6 | 3 | 2001 | 30 |
6b+4h | 6 | 4 | 1252 | 40 |
6b+5h | 6 | 5 | 785 | 60 |
6b+6h | 6 | 6 | 454 | 100 |
6b+7h | 6 | 7 | 752 | 400 |
6b+8h | 6 | 8 | 617 | 600 |
7b+8h | 7 | 8 | 597 | 900 |
8b+8h | 8 | 8 | 601 | 1000 |
9b+8h | 9 | 8 | 657 | 1200 |
10b+8h | 10 | 8 | 621 | 1200 |
11b+8h | 11 | 8 | 623 | 1200 |
12b+8h | 12 | 8 | 522 | 1200 |
本底的测量 | 0 | 0 | 120 | 300 |
I0的测量 | 0 | 0 | 13702 | 30 |
其中,铝箔的质量厚度中,b表示每一薄片的质量厚度,h表示每一厚片的质量厚度; | ||||
经过计算,可得: 每一薄片的质量厚度 每一厚片的质量厚度 | ||||
3. 绘制吸收曲线,并求出R和EMAX:
绘制吸收曲线 | |||||
I/I0 | 0.893 | 0.823 | 0.741 | 0.695 | 0.650 |
d/mgNaN-2 | 18.838 | 37.676 | 56.514 | 75.352 | 94.190 |
I/I0 | 0.613 | 0.419 | 0.263 | 0.145 | 0.0677 |
d/mgNaN-2 | 113.082 | 221.060 | 329.092 | 437.124 | 545.156 |
I/I0 | 0.0278 | 0.00907 | 0.00324 | 0.00137 | 0.000577 |
d/mgNaN-2 | 653.188 | 761.220 | 869.252 | 977.284 | 996.122 |
I/I0 | 0.000440 | 0.000323 | 0.000257 | 0.000261 | 7.67E-05 |
d/mgNaN-2 | 1014.960 | 1033.798 | 1052.636 | 1071.475 | 1090.312 |
此处的I和I0均为减去本底以后的数值,d的数值由上表方法计算而得; | |||||
吸收曲线
| |||||
得到P点坐标为 | |||||
由此进行计算如下: β射线射程 满足条件R>0.3g/cm2 因此, | |||||
实验小结及建议:
本实验是一个比较好的实验,引起误差的主要因素有如下述:一则,计数器显示的计数偶尔会出现跳数,可能是由于放射源本身的随机误差,也可能是由于外界影响造成计数管不稳定产生的误差;其次,铝箔的放置和铝箔本身的偏差都对实验造成影响;另外,测量时间也各有不同,造成了计数的标准不严格统一;,曲线外推有主观性,难免造成误差!
从本次实验的结果来看,实验测得的吸收曲线与理论情况比较符合,中间段相关系数达到0.99346,线性较好,与理论基本符合;首尾部分的偏离的原因可能是由于电离损失,軔致辐射,多次辐射,以及同时放出X射线等造成的影响。
总的来说,实验结果基本让人满意,在现有实验条件下,实验比较准确。
思考题:
1. 在测量吸收曲线时,放射源、吸收物质、探测器等的相对位置以及工作条件等是否可以改变?为什么?
答:
不可以改变,一方面,源、吸收物质、探测器等的相对位置决定了在时间里实验探测到的粒子数的强弱多少,若相对位置改变则可能造成探测器没有对准放射源、或者铝箔位置不正,造成探测到的粒子数不反映普遍规律。另一方面,β射线的能量衰减包括了电离损失,軔致辐射,多次辐射等,相对位置和

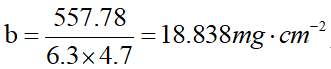 ;
;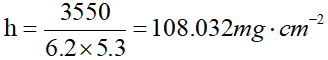 ;
;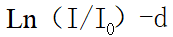 作图如下:
作图如下: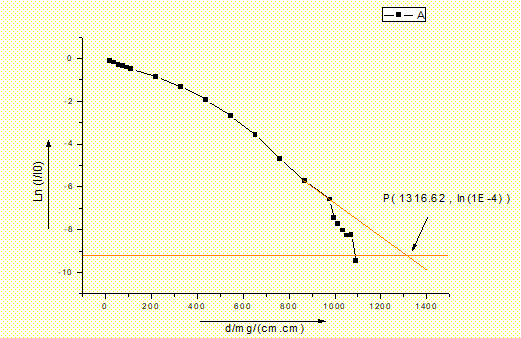 坏点应舍去不计
坏点应舍去不计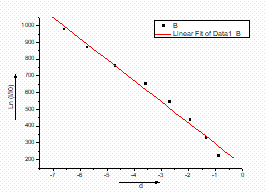 由上图看出I/I0总体上基本满足指数衰减的趋势,舍弃首尾点以后,中间段的相关系数达到了0.99346(见左图),说明中间段的线性较好;为按直线外推至I/I0为10-4提供了合理的依据;
由上图看出I/I0总体上基本满足指数衰减的趋势,舍弃首尾点以后,中间段的相关系数达到了0.99346(见左图),说明中间段的线性较好;为按直线外推至I/I0为10-4提供了合理的依据;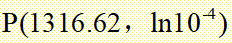
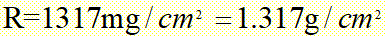 ;
;
